今日は、勝負どころの関数の問題です。
関数も、頭を柔軟にして、とり組まないといけません。
今年も、速さの問題でした。
グラフで電車の動きをイメージできる力が必要です。

（3）の問題の概要
与えられたグラフは、電車Ｐが8時にＡを出発し、Ｂ駅で３分停車した後、Ｃ駅に8時20分に到着した様子を示しています。
これに対して、電車Ｑは、８時４分にＡを出発し同じ速さでＣ駅向かいます。
電車Ｑは、電車ＰがＢ駅に到着した後にＢ駅を通過し、電車Ｐより早くＣ駅する。
電車Ｑの速度は、分速何ｍより速く、分速何ｍより遅いかを聞いています。

これも、問題の本質が、グラフのイメージとしてつかめなければ解けない問題です。
最も速いときと遅いときとは、それぞれどこを通る場合か、がポイントとなります。

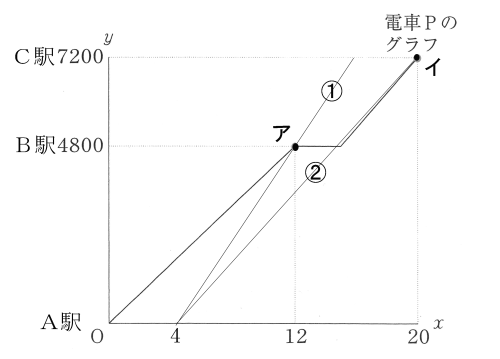
速いときは、アの点を通る①、遅い場合は、イの点を通る②になります。
それぞれの傾きを出せば終わりです。

最後の問題は、高度です。

しかも、２つの式が
電車Ｐの式は、ｙ＝480ｘ－2400　で、
これでも、数がでかいのですが、
電車Ｒの式は、ｙ＝－320ｘ＋11680　となるので、
このあとの、
480ｘ－2400＝－320ｘ＋11680
を解くのは大変です。

算数で、
電車ＰがＢ駅を出発する８時１５分のときの、双方の距離を求めて、
両方の速さで割ったほうが簡単に出来ます。

今年の問題では、他に累積度数の問題で
２桁割る２桁の計算を小数第２位まで求める計算を３つさせています。

今の生徒たちの中には、小数の計算がおぼつかない子も少なくありません。
しっかりとして計算力をつけておくことも大切です。